Representation Theory

Some definitions to build enough structure to talk about symmetries in physics by thinking of symmetry groups like shapes that partition space and time.

**Suggested Reading Order: Geometry > Forms > Lie Crap > ** You are Here

---

Representation Definitions

Representations are maps that take you from a Lie Group, or a Lie algebra, to a place that contains transformations of a vector space. In other words it is a way to interpret the elements of a Lie group as the actual actions that would turn adn reshape the vector space.

Defintion: Let $G$ be a Lie group and $V$ a vector space over the field $\mathbb{K}\in \{\mathbb{R},\mathbb{C}\}$. Then a representation of $G$ on $V$ is a group homomorphism $\rho$ given by

$$\begin{gathered} \rho :G\to GL(V) \\ g\in G\mapsto \rho (g)\in GL(V) \end{gathered}$$

We denote by $GL(V)$ the linear automorphism group of the vector space $V$. In other words the group, under composition, of maps from $V\to V$ that are linear isomorphisms. Note that $GL(V)$ is a Lie Group. One can prove this by viewing $GL(V)$ as a matrix group and then realizing that matrix groups are isomorphic to ${\mathbb{R}}^{n^2}$. More to the point we can say that

$$GL(V)\cong GL(\dim V,\mathbb{K})$$

Where this is the general linear goup over the equivalent field.

Notation: When the representation $\rho$ is clear from context we often write for $g\in G$ and $v\in V$

$$\rho (g)v=g\cdot v=gv$$

Defintion: A representation $\rho$ is faithful iff it is injective.

Remark: Notice that since a Lie Group representation $\rho$ is a homomorphism we have that for any $g,h\in G$

1. $\rho (gh)=\rho (g)\circ \rho (h)$
2. $\rho (g^{-1})=\rho (g{)}^{-1}$

Definition: Given two representations ${\rho }_V$ and ${\rho }_W$ of Liw group $G$ to the vector spaces $V$ and $W$ respectively, a morphism $f$ is a linear map such that

$$\begin{gathered} f:V\to W \\ f({\rho }_V(g)v)={\rho }_W(g)f(v),\mathrm{\forall }v\in V,\mathrm{\forall }g\in G \end{gathered}$$

in simpler notation

$$f(gv)=gf(v)$$

If the map is also an isomorphism of vector spaces it is called an isomorphism or an equivalence of representations for some reason.

Now we copy paste for a Lie Algebra. Because we also want to do this for the algebras.

Definition: Let $\mathfrak{g}$ be the Lie Algebra of Lie Group $G$ and $V$ some vector space over field $\mathbb{K}$. A representation of the Lie Algebra $\varphi$ is a Lie algebra homomorphism

$$\varphi :\mathfrak{g}\to \mathfrak{gl}(V)\cong \text{End}(V)$$

Where $\text{End}(V)$ denotes the set of linear endomorphisms of $V$, these are linear maps from $V\to V$. Notice that they don’t have to be invertible (i.e. isomorphisms). With the representation of the group we are mapping to the set of Automorphisms $GL(V)\subset \text{End}(V)$. Notice that the automorphisms are also a subgroup under composition.

Defintion: A lie algebra representation $\varphi$ is faithful iff it is injective.

Remark: Since the representation $\varphi$ is a lie algebra homomorphism we have that

$$[\varphi (X),\varphi (Y)]=\varphi (X)\circ \varphi (Y)-\varphi (Y)\circ \varphi (X)$$

Definition: Given two representations ${\varphi }_V$ and ${\varphi }_W$ of Lie Algebra $\mathfrak{g}$ to the vector spaces $V$ and $W$ respectively, a morphism $f$ is a linear map such that

$$\begin{gathered} f:V\to W \\ f({\varphi }_V(X)v)={\varphi }_W(X)f(v),\mathrm{\forall }v\in V,\mathrm{\forall }X\in \mathfrak{g} \end{gathered}$$

in simpler notation

$$f(Xv)=Xf(v)$$

If the map is also an isomorphism of vector spaces it is called an isomorphism or an equivalence of Lie Algebra representations.

Proposition: Let $\rho :G\to GL(V)$ be a Lie Group representation then the pushforward of $\rho$ is a Lie Algebra representation ${\rho }_{\ast }:\mathfrak{g}\to \mathfrak{gl}(V)\cong \text{End}(V)$.

In particular take a look at this diagram and now we can move around it.

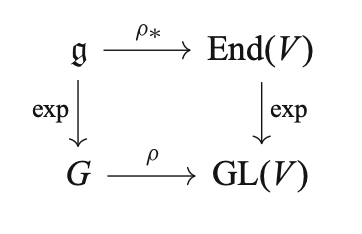
This implies that for any vector field $X\in \mathfrak{g}$ we can write its representation as

$$\rho (\exp X)=e^{{\rho }_{\ast }X}\in GL(V)$$

We will see that this will later correspond to moving along our symmetries with a some operator.

Definition: Under any representation $\rho$ of a Lie Group $G$ (or its Lie algebra) on a vector space $V$ over $\mathbb{K}$, an invariant subspace $W\subset V$ is a subspace of $V$ such that $G\cdot W\subset W$ ($\mathfrak{g}\cdot W\subset W$).

Definition: A representation $\rho$ of a Lie Group $G$ (or its Lie algebra) on a vector space $V$ over $\mathbb{K}$ is irreducible iff threre is no proper invariant subspace $W\subset V$. Otherwise it is reducible

This is really important. In particle physics we define a particle as an irreducible representation of the symmetry group of the theory. Later we will define another way of finding irreducible representations, but for now this should be ok. What it says is that you can take a vector in V where there is some element in $G$ that can map it out of whatever subspace you choose.

Representation Flavours

A quick list of ways to describe representations using your favourite set and space operations.

Definition: Let $V,W$ be vector spaces with representations

$$\begin{gathered} {\rho }_V:G\to GL(V) \\ {\rho }_W:G\to GL(W) \end{gathered}$$

of some Lie group $G$. Then we can define the follwoing representations of $G$ $\mathrm{\forall }g,h\in G,\mathrm{\forall }v\in V,\mathrm{\forall }w\in W$.

1. Direct Sum: ${\rho }_{V\oplus W}$ on $V\oplus W$ given by

   $$g(v,w)=(gv,gw)$$

2. Tensor Product: ${\rho }_{V\otimes W}$ on $V\otimes W$ Given by

   $$g(v\otimes w)=(gv)\otimes (gw)$$

3. Dual: ${\rho }_{V^{\vee }}$ on $V^{\vee }$ given by

   $$(gu)(v)=u(g^{-1}v)\mathrm{\forall }u\in V^{\vee }$$

4. Exterior Power: ${\rho }_{\stackrel{k}{\bigwedge }V}$ on $\stackrel{k}{\bigwedge }V$ given by

   $$g(v_1\wedge v_2\wedge \cdots \wedge v_n)=g{v}_1\wedge g{v}_2\wedge \cdots \wedge g{v}_n$$

6. Complex Conjugate: ${\rho }_{V^{\ast }}$ on $V^{\ast }$ given by

   $${\rho }_{V^{\ast }}(g)=({\rho }_V(g)v{)}^{\ast }$$

7. Homomorphism Space: ${\rho }_{\text{Hom}(V,W)}$ on $\text{Hom}(V,W)$ given by

   $$(gf)(v)=gf(g^{-1}v),\mathrm{\forall }f\in \text{Hom}(V,W)$$

8. Outer Product: ${\rho }_V\otimes {\tau }_W$ on $V\otimes W$ for some reprentation ${\tau }_W$ of Lie Group $H$ given $\mathrm{\forall }h\in G$ by

   $$(g,h)(v\otimes w)=gv\otimes gw$$

You can define the same representations for ones that are from Lie Algebras, but I am not going to write them down. In any case, they all act as one would expect, so we just want to use them as tools.

Representing in Inner Product spaces

A vector space $V$ over $\mathbb{K}$ with an inner product $⟨\cdot ,\cdot ⟩:V\times V\to \mathbb{K}$ is a very useful tool in physics as such spaces can help us extract scalar quantities, such as angles or distances, out of the vector space.

Definition: An inner product $⟨\cdot ,\cdot ⟩:V\times V\to \mathbb{K}$ over $V$ can be of many categories, two of which are:

1. Euclidean: Bilinear, symmetric, and positive definite.
2. Hermitian: Complex linear in the second argument while complex antilinear on the first, conjucate symmetric, and postive definite.

The second is the notion of distance that lets us construct unitary operators in the Hilbert spaces encountered in Quantum Mechanics.

Definition: A representation $\rho :G\to GL(V)$ of a Lie group $G$ to a vector space $V$ with a Euclidean (Hermitian) inner product is called orthogonal (unitary) iff

$$⟨gv,gw⟩=⟨\rho (g)v,\rho (g)w⟩=⟨v,w⟩$$

for all $g\in G$ and $v,w\in V$. This means that the image of $\rho$ stays within the orthogonal subgroup $O(V)<GL(V)$ (unitary subgroup $U(V)<GL(V)$) as determined by the inner product $⟨\cdot ,\cdot ⟩$. This inner product is called G-invariant.

Similarly we copy paste for representations of Lie algebras

Definition: A representation $\varphi :\mathfrak{g}\to \text{End}(V)$ of a the Lie algebra of $G$ to a vector space $V$ with a Euclidean (Hermitian) inner product is called skew-symmetric (skew-hermitian) iff

$$⟨Xv,w⟩+⟨v,Xw⟩=⟨\varphi (X)v,w⟩+⟨v,\varphi (X)w⟩=0$$

for all $g\in G$ and $v,w\in V$. This means that the image of $\rho$ stays within the orthogonal lie subalgebra $\mathfrak{o}(V)<\mathfrak{gl}(V)$ (unitary Lie subalgebra $\mathfrak{u}(V)<\mathfrak{gl}(V)$) as determined by the inner product $⟨\cdot ,\cdot ⟩$.

And as one might expect, we state this with proof as an exercise.

Proposition: Let $\rho :G\to GL(V)$ be a representation of Lie group $G$ and $⟨\cdot ,\cdot ⟩$ a $G$-invariant Euclidean (Hermitian) inner product on $V$, i.e. $\rho$ is orthogonal (unitary) on $V$. Then the induced Lie algebra representation ${\rho }_{\ast }$ is skew-symmetric (skew-hermitian).

Now for some physics terms (finally).

Definition: Let $\varphi :\mathfrak{g}\to \text{End}(V)$ be a skew-hermitian (we also sometimes refer to it as unitary for some reason making the definitions aobove infinitely more confusing) representation of a real Lie algebra $\mathfrak{g}$ on some complex vector space $V$. Then $\mathrm{\forall }X\in \mathfrak{g}$ $\varphi (X)$ is a skew hermitian endomorphism, implying that $i\varphi (X)$ is a hermitian endomorphism (notice that this endomorphism is actually invertible since $\varphi$ is skew hermitian). We call the eigenvalues of $-i\varphi (X)$ the charges of $X$ in the representation $\varphi$.

The negative sign is obviously a convention originating form the fact that positive charge is positive.

Definition: A

Decomposition of Representations

Wwe have finally heard the word charge! We will apply this to the context of physics in the future, but for now we need to describe particles. As a result, we need to have a mechanism of describing irriducible representations.

Theorem: Given a representation $\rho :G\to GL(V)$ of a compact Lie group G to a vector space $V$ over the field $\mathbb{K}$ with a $G$-invariant inner product $⟨\cdot ,\cdot ⟩$, $\rho$ can be decomposed to the following direct sum representation

$${\rho }_V={\rho }_{V_1}\oplus {\rho }_{V_2}\oplus \cdots \oplus {\rho }_{V_k}$$

where ${\rho }_{V_i}$ is an the restriction of representation of $G$ on the subspace $V_i$ of $V$. We also have that

$$V=V_1\oplus V_2\oplus \cdots \oplus V_k.$$

Proof: If $\rho$ is reducible $\mathrm{\exists }W\subset V$ such that $G\cdot W\subset W$. Consider the orthogonal complement $W^{\perp }:=\{v\in V|⟨v,u⟩=0\mathrm{\forall }u\in W\}$ (which is also a subgroup with the property that $V=W\oplus W^{\perp }$) . We will show that $G\cdot W^{\perp }\subset W^{\perp }$.

Let $g\in G$ and $w\in W^{\perp }$ such that $gw\in W$. We know that $\mathrm{\exists }v=gu\in W$ for some $u\in W$. Then we have that

$$⟨gv,gw⟩=⟨v,w⟩=0$$

since $w\in W^{\perp }$. Since $W\cap W^{\perp }=\mathrm{\varnothing }$ we have a contradiction.

As a result, it is possible to write the representation as

$$\rho ={\rho }_W\otimes {\rho }_{W^{\perp }}$$

where ${\rho }_W$ is irreducible, and $V=W\otimes W^{\perp }$. Therefore, we can repeat this process until we have reached the direct product of irriducible representations. $◻$

Adjoints (ew but important)

In groups we have multiple fundamental operations. Multiplying from the left, multiplying from the right, and conjugation which is given by the following map

$$\begin{gathered} c_g:G\to G \\ x\mapsto gx{g}^{-1} \end{gathered}$$

Even though it looks stupid, there is some merit to this map as it creates an automorphism of the lie algebra by taking its pushforward $c_{g\ast }$.

So this map will take a vector at some tangent space $T_{x}G$ and it will give you a vector on the same tangent space! so it can also do this for the Lie algebras (the tangent space at the identity).

Theorem: The map

$$\begin{gathered} \text{Ad}:G\to GL(\mathfrak{g}) \\ g\mapsto \text{Ad}(g)={\text{Ad}}_g=c_{g\ast } \end{gathered}$$

is a Lie group homomorphism, i.e. a representation of the Lie group $G$ on the vector space $\mathfrak{g}$ called the adjoint representation or adjoint action of the Lie Group G.

The proof is just calculation from the axioms of a representation.

The reason why we calll this the adjoint representation is because it has the properites that one would expect when reversing the composition. Basically:

Proposition: Given a Lie group representation $\rho$ on a vector space $V$ and some $g\in G$ we have that

$$\rho (g)\circ {\rho }_{\ast }(X)={\rho }_{\ast }({\text{Ad}}_{g}X)\circ \rho (g),\mathrm{\forall }X\in \mathfrak{g}$$

Theorem: The map

$$\begin{gathered} \text{ad}:\mathfrak{g}\to \text{End}(\mathfrak{g}) \\ ad=A{d}_{\ast } \end{gathered}$$

is a Lie algebra homomorphism, i.e. a repersentation of the Lie Algebra $\mathfrak{g}$ on itself as a vector space. This is called the Adjoint representation of the Lie algebra $\mathfrak{g}$.

Corollary: For any Lie algebra $\mathfrak{g}$ the adjoint of the Lie algebra $\text{ad}$ is given by

$$\begin{gathered} ad:\mathfrak{g}\to \text{End}(\mathfrak{g}) \\ {\text{ad}}_{X}Y=[X,Y] \end{gathered}$$

This leads us to talk about metrics on Lie groups that are invariant under certain representations.

Definition: Let $s$ be a metric on the Lie Group $G$. Then it is called:

1. Left Invariant: if $L_g^{\ast }s=s,\mathrm{\forall }g\in G$

2. Right Invariant: if $R_g^{\ast }s=s,\mathrm{\forall }g\in G$

3. Bivariant: if it is both left and right invariant. : )

Note: Given any metric $s$ on $G$ we can always define an inner product on $\mathfrak{g}$ using the metric like so

$$\begin{gathered} ⟨\cdot ,\cdot ⟩:\mathfrak{g}\times \mathfrak{g}\to \mathbb{K} \\ ⟨X,Y⟩=s(X,Y) \end{gathered}$$

We could make thi matric left invariant by taking the left translation map, or right invariant by using the right translation map. However, in general, to get a bivariant metric $G$ hsd to be abelian.

Theorem: Let $s$ be a left invariant metric on Lie group $G$. Then $s$ is bi-invariant iff the inner product on $\mathfrak{g}$ defined by the metric $s$ is $\text{Ad}$-invariant, i.e.

$$⟨{\text{Ad}}_{g}X,{\text{Ad}}_{g}Y⟩=⟨X,Y⟩,\mathrm{\forall }g\in G\text{ and }\mathrm{\forall }X,Y\in \mathfrak{g}$$

Theorem: Let $G$ be a compact Lie group. Then there exists aEuclidean scalar product on the Lie algebra $\mathfrak{g}$ which is $\text{Ad}$-invariant. The adjoint representation is orthogonal with respect to this scalar product.

Corollary: Every compact Lie group can have a bi-invariant Riemannian metric.

The Killing Form

Not all $\text{Ad}$-invariant inner products are created equal. There is a special one that we use all the time to characterize symmetries. We call that the Killing form.

Theorem: Let $\mathfrak{g}$ be a Lie Algebra over the field $\mathbb{K}$. The Killing form $B$ on $\mathfrak{g}$ is defined by

$$\begin{gathered} B_g:\mathfrak{g}\times \mathfrak{g}\to \mathbb{K} \\ (X,Y)\mapsto tr({\text{ad}}_X\circ {\text{ad}}_Y). \end{gathered}$$

This is a bilinear, symmetric form on $\mathfrak{g}$.

Proof: Consider $Z\in \mathfrak{g}$, then

$${\text{ad}}_X\circ {\text{ad}}_Y(Z)=[X,[Y,Z]]$$

This shows that the killing form is bilinear. To show that it is symmetric we have to prove some properties of the trance.

For an arbitrary linear endomorphism $f\in \text{End}(\mathfrak{g})$ and a basis $v_i$ for $\mathfrak{g}$ we have that

$$f(v_j)=f_j^i{v}_i$$

and that

$$\text{tr}(f)=f_i^i$$

Now consider a linear isomorphism $\varphi \in \text{End}(\mathfrak{g})$ we can change the basis of $\mathfrak{g}$ simply by performing $\varphi \circ f\circ {\varphi }^{-1}$. We can show that the trace is invariant to this as:

$$\begin{array}{rl}\text{tr}(\varphi \circ f\circ {\varphi }^{-1})& =(\varphi \circ f{)}_j^i({\varphi }^{-1}{)}_i^j\\ & =({\varphi }^{-1}{)}_j^i(\varphi \circ f{)}_i^j\\ & =\text{tr}(\varphi \circ {\varphi }^{-1}\circ f)\\ & =\mathrm{tr}\left(f\right)\end{array}$$

Therfore, we know that the trace is symmetric.

Note: The Killing form for Complex Lie Algebras is not Hermitian.

Theorem: Let $\sigma :\mathfrak{g}\to \mathfrak{g}$ be a Lie algebra automorphism of $\mathfrak{g}$. Then the Killing form $B$ satisfies the following

$$B(\sigma X,\sigma Y)=B(X,Y)$$

A nice application of this theorem is the fact that the Killing form is invariant under the Lie algebra automorphism ${\text{Ad}}_g\mathrm{\forall }g\in G$.

Corollary: The killing form $B$ defines a bi-invariant symmetric form on any Lie group $G$.